Figure 1.
In high school math, you might have learnt a trick for evaluating integrals like
$$\int{1\over x^2+3x+2}.$$
This trick is called partial fractions, and it involves rewriting the fraction as a sum of simpler fractions whose integrals are already known. In this case,
$$ \begin{align*} \int{1\over x^2+3x+2} &= \int{1\over(x+1)(x+2)} \\ &= \int\left({1\over x+1}-{1\over x+2}\right) \\ &= \int{1\over x+1}-\int{1\over x+2} \\ &= \ln|x+1| - \ln|x+2| + C. \end{align*} $$
The same trick can be applied to more complicated expressions. For instance,
$$ \begin{align*} \int{x^5+11x^4+50x^3+114x^2+132x+66\over x^6+14x^5+80x^4+238x^3+387x^2+324x+108} &= \int{1\over x+1}-\int{2\over(x+2)^2}+\int{3\over(x+3)^3} \\ &= \ln|x+1|+{2\over x+2}-{3\over2(x+2)^2}+C. \end{align*} $$
Naturally, one should ask if this trick always applies to an expression of the form $(\text{polynomial}/\text{polynomial})$, called a rational function. The answer is yes! Specifically, I will show in this post that every rational function can be written as a sum of a polynomial and partial fractions of the form
$$\begin{equation}\label{1}{A\over(x-B)^k} \quad\text{or}\quad {Ax+B\over(x^2+Cx+D)^k}.\end{equation}$$
The former is easy to integrate via the power rule, while the latter is more difficult but can be tamed by standard substitutions. (I might go through this in a future post.)
I recommend skipping to the worked example to see the procedure in action, then consulting the preceding text for theoretical justifications.
I'll write $P(x)$ to denote a rational function. $P(x)$ is usually thought of as a function on the real numbers, but let's broaden our perspective by allowing complex-valued inputs and outputs. (To emphasise the point, we'll use $z$ as the input). Then we can make use of tools from complex analysis.
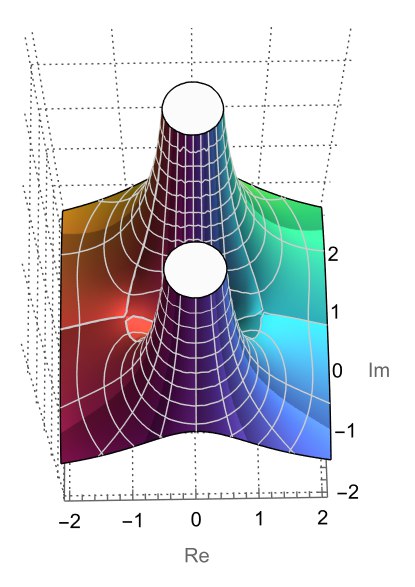
For example, plugging in $z=2i$ into the rational function $P(z)=z/(z^2+1)$ gives the output $-2i/3$. In fact, we can make a 3D plot showing the absolute value of each output:

|
Figure 1. |
Note how the graph blows up near the points $\pm i$ (these are called poles). This is because the denominator factors as $(z+i)(z-i)$, and the product tends to 0 (so its absolute value also tends to 0) whenever $z$ approaches $i$ or $-i$.
In general, the fundamental theorem of algebra tells us that the denominator always factors as a product of the form
$$(z-c_1)^{k_1}(z-c_2)^{k_2}\dots(z-c_n)^{k_n}.$$
By definition, the $c_i$'s are the roots of the denominator (equivalently, the poles of the rational function), and its associated $k_i$ is called the order.
Let's focus on some particular $c_i$; for convenience I'll drop the subscript. We know $P(z)$ blows up here because of the $(z-c)^k$ factor in the denominator. We can cancel it out by multiplying $P(z)$ by $(z-c)^k$. The function $(z-c)^kP(z)$ no longer has a pole at $c$, and therefore complex analysis tells us we can expand it as a power series around $c$1:
$$(z-c)^kP(z) = a_0 + a_1(z-c) + a_2(z-c)^2 + \ldots$$
Dividing both sides by $(z-c)^k$ gives us a helpful new way of looking at $P(z)$:
$$\begin{equation}\label{2}P(z) = a_0(z-c)^{-k} + a_1(z-c)^{-k+1} + a_2(z-c)^{-k+2} + \ldots\end{equation}$$
Now, we see that $P(z)$ blows up at $c$ due to the terms where $(z-c)$ appears in the denominator:
$$a_0(z-c)^{-k}+a_1(z-c)^{-k+1}+\ldots+a_{k-1}(z-c)^{-1}.$$
Subtracting away these terms leaves us with the series
$$a_k + a_{k+1}(z-c) + a_{k+2}(z-c)^2 + \ldots,$$
which approaches the finite value $a_k+0+0+\ldots$ when $z\to c$ — no more pole! (Notice that we've cancelled a pole two different ways.)
This subtraction process can be done for every pole $c_i$. Start by expanding $P(z)$ in the form $\eqref{2}$ around $c_1$, and subtract away the negative-power terms $(z-c_1)^{-i}$. That leaves us with a function $P_1(z)$ with poles $c_2,\ldots,c_n$. Then repeat the process with $P_1(z)$ and $c_2$, and so on. At the end, we are left with some rational function with no poles, namely a polynomial2 $p(z)$. In symbols,
$$P(z) - \sum_{i=1}^{k_1}{a_{1i}\over(z-c_1)^i} - \ldots - \sum_{i=1}^{k_n}{a_{ni}\over(z-c_n)^i} = p(z).$$
Bringing all the sums to the right side, we actually get something very close to the partial fraction expansion of $P(z)$. The snag is that the $c_i$'s are complex, but when our $P(z)$ is real, we also want the partial fractions to be real.
We can fix this with some work, using the fact that the roots $c_1,\ldots,c_n$ come in conjugate pairs, i.e. if $c$ is a root then $\overline c$ is also a root with the same order3. Thus, for any non-real $c$ we can group the negative-power terms for $c$ and $\overline c$ in pairs:
$$\begin{align*}\sum_{i=1}^k{a_i\over(z-c)^i} + \sum_{i=1}^k{b_i\over(z-\overline c)^i} &= \sum_{i=1}^k {a_i\over(z-c)^i}+{b_i\over(z-\overline c)^i} \\ &= \sum_{i=1}^k {a_i(z-\overline c)^i+b_i(z-c)^i\over (z^2-2\Re(c)z+|c|^2)^i}. \end{align*}$$
Note that the denominator has real coefficients. However, we are not done because looking at \eqref{1}, the numerators have to be linear. To achieve this, we do a polynomial division4 of
$$a_i(z-\overline c)^i+b_i(z-c)^i \quad\text{by}\quad z^2-2\Re(c)z+|c|^2,$$
thus obtaining
$${p(z)\over (z^2-2\Re(c)z+|c|^2)^{i-1}} + {Az+B\over(z^2-2\Re(c)z+|c|^2)^i}.$$
The coefficients $A,B$ can be shown to be real5, and the first term is a sum of terms of the second type in \eqref{1} by induction. Thus,
$$\sum_{i=1}^k {a_i(z-\overline c)^i+b_i(z-c)^i\over (z^2-2\Re(c)z+|c|^2)^i}$$
is overall a sum of terms of the second type in \eqref{1}. Finally, repeating this combining process for all pairs of conjugate roots $c,\overline c$ gives us the result at \eqref{1}.
As mentioned above, to obtain the partial fraction decomposition of $P(z)$, we have to subtract off the negative-power terms of
$$P(z) = a_0(z-c)^{-k}+\ldots+a_{k-1}(z-c)^{-1}+a_k+a_{k+1}(z-c)+\ldots$$
for each pole $c$. In particular, we need to find the values of $a_0,\ldots,a_{k-1}$. To do this, we cleverly substitute $1/z+c$ for $z$, thus turning $P(z)$ 'inside-out':
$$P(1/z+c) = (a_0z^k+\ldots+a_{k-1}z+a_k)+(a_{k+1}z^{-1}+\ldots)$$
Then, our desired coefficients are obtained by writing $P(1/z+c)$ in the form $p(z)/q(z)$ where $p(z),q(z)$ are polynomials, and then computing the quotient of $p(z)$ divided by $q(z)$ (which is the first bracketed term). Note that the constant coefficient $a_k$ is ignored in the quotient.
In the case where $P(z)$ is real, we need to perform additional polynomial divisions by $(z-c)(z-\overline c)$ as mentioned above.
Let's try to expand $$P(z)={z^4\over z^5-z^4+2z^3-2z^2+z-1}$$ in partial fractions. First, factorise the denominator to obtain
$$z^5-z^4+2z^3-2z^2+z-1 = (z+i)^2(z-i)^2(z-1).$$
Thus the poles are $\pm i$ (order 2) and 1 (order 1). Let's first handle $z=1$; the expansion of $P(z)$ looks like
$$P(z) = {a_0\over z-1}+a_1+a_2(z-1)+\ldots.$$
To find $a_0$, we compute the numerator and denominator of $P(1/z+1)$6:
$$P\left(1/z+1\right) = {z^5+4z^4+6z^3+4z^2+z\over 4z^4+8z^3+8z^2+4z+1};$$
dividing the numerator by the denominator gives a quotient of $z/4+1/2$. Therefore $a_0=1/4$ and the partial fraction corresponding to $z=1$ is $1/4(z-1)$.
Similarly for $z=i$ we have
$$P\left(1/z+i\right) = {iz^5+4z^4-6iz^3-4z^2+iz\over (4+4i)z^3+(4-8i)z^2-(5+i)z+i},$$
and the quotient is $(1/8+i/8)z^2+(3/8-i/4)z+(-1/32-9i/32)$, so the partial fractions corresponding to $z=i$ are
$${{3\over8}-{i\over4}\over z-i} + {{1\over8}+{i\over8}\over(z-i)^2}.$$
The same computation could be done for $z=-i$, but actually we can save all the work by noting that the coefficients are simply conjugated:
$${{3\over8}+{i\over4}\over z+i} + {{1\over8}-{i\over8}\over(z+i)^2}.$$
Putting all the partial fractions together gives us
$$P(z) = {1/4\over z-1} + {{3\over8}-{i\over4}\over z-i} + {{1\over8}+{i\over8}\over(z-i)^2} + {{3\over8}+{i\over4}\over z+i} + {{1\over8}-{i\over8}\over(z+i)^2}.$$
If we insisted on only having real numbers, then the terms $1/(z\pm i)$ and $1/(z\pm i)^2$ need to be combined. Adding the $1/(z\pm i)$ terms:
$${{3\over8}+{i\over4}\over z+i} + {{3\over8}-{i\over4}\over z-i} = {3z/4+1/2\over z^2+1};$$
the right-hand side fraction has the form $(Az+B)/(z^2+Cz+D)^k$ so we are done. As for the $1/(z\pm i)^2$ terms:
$${{1\over8}-{i\over8}\over(z+i)^2} + {{1\over8}+{i\over8}\over(z-i)^2} = {z^2/4-z/2-1/4\over(z^2+1)^2}.$$
The numerator is not linear, so divide $z^2/4-z/2-1/4$ by $z^2+1$ to get the quotient $1/4$ and remainder $-z/2-1/2$. Then we split the right-hand side fraction as
$${1/4\over z^2+1} + {-z/2-1/2\over(z^2+1)^2}.$$
Adding up the $1/(z^2+1)$ and $1/(z^2+1)^2$ terms, we finally obtain the real partial fraction expansion
$$P(z) = {1\over 4(z-1)} + {3\over4}{z+1\over z^2+1} - {1\over2}{z+1\over(z^2+1)^2}.\;\qed$$